Building micrograd
Following up on my self development plans, I recently went through the YouTube video for Andrej Karpathy building Micrograd and I found it super fun and interesting!
I chose this video because I have studied single-neuron machine learning approaches such as logistic regressions, and then used multi-layer networks like LLMs and CNNs for larger tasks, without really understanding them in depth. I thought this video would be a good addition because it looks at propagation through a neural network.
It’s also the first video in Andrej’s series, Zero to Hero, where he goes from minimal prerequisites to understanding how a modern LLM works. They’re also just really fun videos, and they’re very well explained.
Micrograd is a small neural network, and in the video he shows you how to create it as a Python object, and how to use backpropagation to train the network on a small dataset. In this blog post, I want to just summarise some of the key things that I learned.
The main takeaway for me was seeing how the gradient is calculated at the nodes going back from the loss function, propagating through to all the leaf nodes. And also realising that any expression could be in a neural network, e.g. tanh, as long as you can work out the derivative.
There are few different parts which I lay out as follows:
- Creating a
Valueobject - Creating a connected graph of values
- Creating a network of neurons
- Backpropagate through the network
- Recap: what did we learn?
Creating the Value object
The first thing we do is create a Value object to act as a wrapper for float values, and to implement some basic operations.
class Value:
def __init__(self, data):
self.data = data
def __repr__(self):
"""Used to return a string representation of an object."""
return f"Value(data={self.data})"
def __add__(self, other):
out = Value(self.data + other.data)
return out
def __mul__(self, other):
out = Value(self.data * other.data)
return out
a = Value(2.0)
b = Value(-3.0)
a *b
Creating a connected graph of values
In order to code up a network, we need to be able to store their connections. We also implement a way to work out the gradient of each node, in terms of its effect on the final output.
So calculating the gradient requires propagating backward. First we have to calculate the gradient of the Values which are closest to the final output.
class Value:
def __init__(self, data, _children=(), _op='', label=''):
self.data = data
self.grad = 0 # we start from assuming the gradient is zero
self._prev = set(_children)
self._op = _op
self.label = label
self._backward = lambda : None # does the function at each node, and for a leaf function there's nothing to do
def __repr__(self):
"""Used to return a string representation of an object."""
return f"Value(data={self.data})"
def __add__(self, other):
"""Python knows that '+' is the same as '__add__' here."""
out = Value(self.data + other.data, (self, other),'+')
def _backward():
# when we just add nodes values together, their local grad is just 1
self.grad = 1.0 * out.grad # out.grad here because that's the grad of the input Value
other.grad = 1.0 * out.grad
out._backward = _backward
return out
def __mul__(self, other):
out = Value(self.data * other.data, (self, other), '*')
def _backward():
# when we multiply node values together, their grads are the other datas
self.grad = other.data * out.grad
other.grad = self.data * out.grad
out._backward = _backward
return out
def tanh(self):
x = self.data
t = (math.exp(2*x) -1 )/(math.exp(2*x) + 1)
out = Value(t, (self,), 'tanh')
def _backward():
self.grad = 1 - t ** 2
out._backward = _backward
return out
Let’s focus on this block which implements addition:
def __add__(self, other):
"""Python knows that '+' is the same as '__add__' here."""
out = Value(self.data + other.data, (self, other),'+')
def _backward():
# when we just add nodes values together, their local grad is just 1
self.grad = 1.0 * out.grad # out.grad here because that's the grad of the input Value
other.grad = 1.0 * out.grad
out._backward = _backward
return out
It’s telling us a few things:
- If a
Valueimplements the plus operation “+”, then the output will be the data from the two input values added together. - When we call
_backward, two gradients will be updated: the gradient of this particular value is equal to the gradients of all the Values downstream of it (closer to the output), represented byself.grad = 1.0 * out.grad. Also the gradient of whatever is being added,other, is similarly updated. Since this is just addition, the derivative will be 1, and so the chain rule of the later impact on the output requires out.grad.
If we compare it with the multiplication block, we get:
def __mul__(self, other):
out = Value(self.data * other.data, (self, other), '*')
def _backward():
# when we multiply node values together, their grads are the other datas
self.grad = other.data * out.grad
other.grad = self.data * out.grad
out._backward = _backward
return out
The gradients are mathematical expressions, e.g. since the derivative of tanh is 1-t**2
def _backward():
self.grad = 1 - t ** 2
We can piece it together using an expression like this:
a = Value(2.0, label='a')
b = Value(-3.0, label='b')
c = Value(10, label='c')
e = a*b; e.label='e'
d = e + c; d.label='d'
f = Value(-2.0, label='f')
L = d * f; L.label='L'
This now gives us a connected set of values as shown below.

Creating a network of neurons
To make this into a proper neural network, we implement neurons, which require inputs $x_i$ and the weights $w_i$. Both the input data and the weights values, which means we’ll get a load of derivatives for the inputs, which won’t be useful. But I suppose it means we can use one class for both data types.
class Neuron:
def __init__(self, nin):
"""
The constructor.
nin is the number of inputs
The weights are randomly initialised for all of its inputs.
This implements sum_i w_i * x_i + b
"""
self.w = [Value(random.uniform(-1, 1)) for _ in range(nin)]
self.b = Value(random.uniform(-1,1))
def __call__(self, x):
# implements w * x + b
# the function that is called when we just invoke an instance of the class directly
"""The forward pass of the neuron is when you compute the prediction."""
act = sum((wi*xi for wi, xi in zip(self.w, x)), start=self.b)
out = act.tanh()
return out
We can then implement a network with several layers and multiple nodes, with many routes between them, like this:
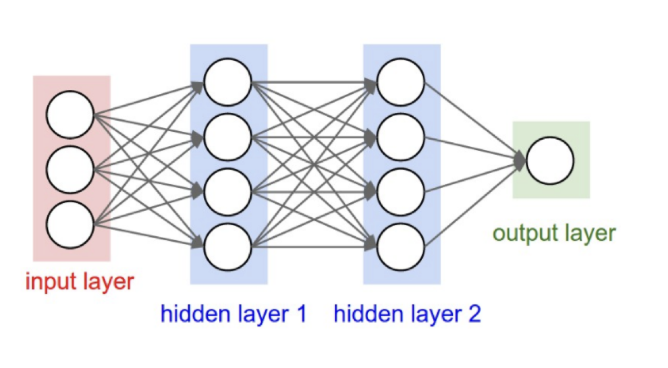
Backpropagate through the network
Once we have definitions for Neuron, Layer, and MLP (multi-layer perceptron), we then define a loss metric, in our case mean square error. Then we can backpropagate through something beautiful: loss.backward()!
# we loop through these three steps:
for k in range(10):
# forward pass to get the predictions
ypred = [n(x) for x in xs]
loss = sum(((yout-ygt) ** 2 for ygt, yout in zip(ys, ypred)), start=Value(0))
# backward pass to get the gradients
for p in n.parameters():
p.grad = 0.0 # we need to reset the gradients to zero, otherwise multiple grads from different runs are added on top of each other, giving a big step size
loss.backward()
# update the weights
for p in n.parameters():
p.data += -0.1 * p.grad
print(k, loss.data)
The loss starts quite high but rapidly converges:
0 7.621655285992237
1 6.8249632743592175
2 2.527103829686314
3 2.214515945507674
4 1.6286164806117236
5 0.4120368073987528
6 0.0742491943612626
7 0.052559211250508275
8 0.04253871146342436
9 0.03590503250488863
Recap: What did we learn?
- Neural nets are mathematical expressions
- We train them using a forward pass, a backward pass, and an update step
- The loss function measures the accuracy of the predictions
- We used backpropagation to get the gradient, working out the gradient for the nodes closest to the output first, then moving backwards
- Using the gradient for each node, we updated each node to tune the weights
- We iterate this process many times in gradient descent
Enjoy Reading This Article?
Here are some more articles you might like to read next: